Math and Physics of Benderama

The last episode of Futurama has interesting formula involved. The entire plot is based on the Professor's latest invention — Banach-Tarski Dupla-Shrinker — the machine that produces two copies of any object at a 60% scale. It was just a matter of time when Bender found a good usage of this machine: to replicate himself. Then two small copies of Bender replicated themselves making four smaller copies, and so forth. At some point the Professor horrified the crew that if they don't stop this unlimited growth, the total mass of all Benders will eventually be so big that the entire Earth will be consumed during the process of replication. As a proof he demonstrated this formula of the mass of all generations of Bender


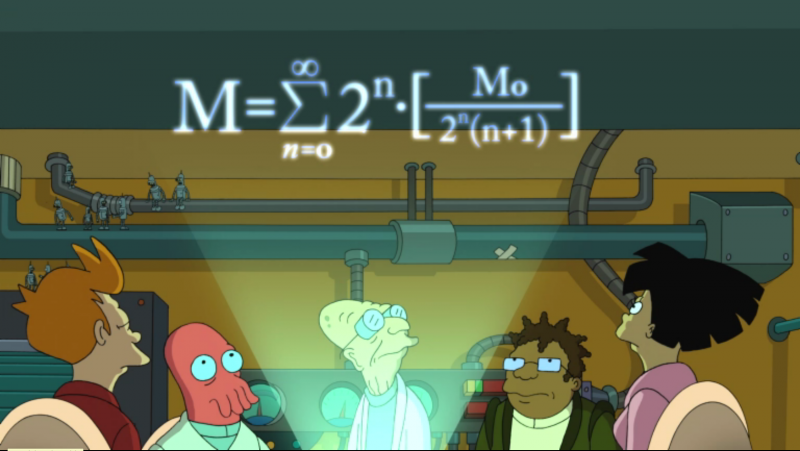
This is a perfect toy for a science geek. The first obvious question it brings: is this formula mathematically correct? As it turns out, it is not. Considering the scale of 60%, the cubic dependency of volume on linear dimension, and the constant density of all copies, the formula should be the following


As you can see the total mass of infinite number of Benders actually converges to approximately 1.76 M₀. So from Math perspective there is nothing to worry about. But what if our assumption of constant density is invalid. Would it be a problem from Physics perspective? Let's see.

Knowing that every new copy has a size of 0.6 of the original it was made from, we have the following formula for the size of Bender in the n^th generation


This exponential function becomes very small pretty soon. In the 154^th generation it already reaches the Planck length, after which the further replication is physically impossible. If we calculate the total mass of 154 Bender's generations using the Professor's formula, we get H(154) × 238 kg ≈ 1,337.56 kg, which is nothing comparing to the Earth mass.

So we have to admit that from both Math and Physics perspective the Professor was wrong, and there was no real threat to the Earth.

Although the Professor's formula doesn't describe the replication process adequately, it's still a beautiful piece of Math because it's a formula of harmonic series. If you want to know why harmonic series is beautiful and which real processes it describes, read this nice article of John H. Webb.

And don't miss the next episode of Futurama this Thursday :-)